Most discussions about sorting algorithms tend to end up discussing quicksort because of its speed. Formal computer science programs also tend to cover quicksort¹ last because of its excellent average complexity of O(n log n) and relative performance improvement over other, less efficient sorting algorithms such as bubble sort and insertion sort for large data sets. Unlike other sorting algorithms, there are many different implementations of quicksort that lead to different performance characteristics and whether or not the sort is stable (with equivalent items remaining in the same order in which they naturally occurred).

Quicksort is a divide and conquer algorithm in the style of merge sort. The basic idea is to find a “pivot” item in the array to compare all other items against, then shift items such that all of the items before the pivot are less than the pivot value and all the items after the pivot are greater than the pivot value. After that, recursively perform the same operation on the items before and after the pivot. There are many different algorithms to achieve a quicksort and this post explores just one of them.

There are two basic operations in the algorithm, swapping items in place and partitioning a section of the array. The basic steps to partition an array are:

1. Find a “pivot” item in the array. This item is the basis for comparison for a single round.
2. Start a pointer (the left pointer) at the first item in the array.
3. Start a pointer (the right pointer) at the last item in the array.
4. While the value at the left pointer in the array is less than the pivot value, move the left pointer to the right (add 1). Continue until the value at the left pointer is greater than or equal to the pivot value.
5. While the value at the right pointer in the array is greater than the pivot value, move the right pointer to the left (subtract 1). Continue until the value at the right pointer is less than or equal to the pivot value.
6. If the left pointer is less than or equal to the right pointer, then swap the values at these locations in the array.
7. Move the left pointer to the right by one and the right pointer to the left by one.
8. If the left pointer and right pointer don’t meet, go to step 1.

As with many algorithms, it’s easier to understand partitioning by looking at an example. Suppose you have the following array:

var items = [4, 2, 6, 5, 3, 9];

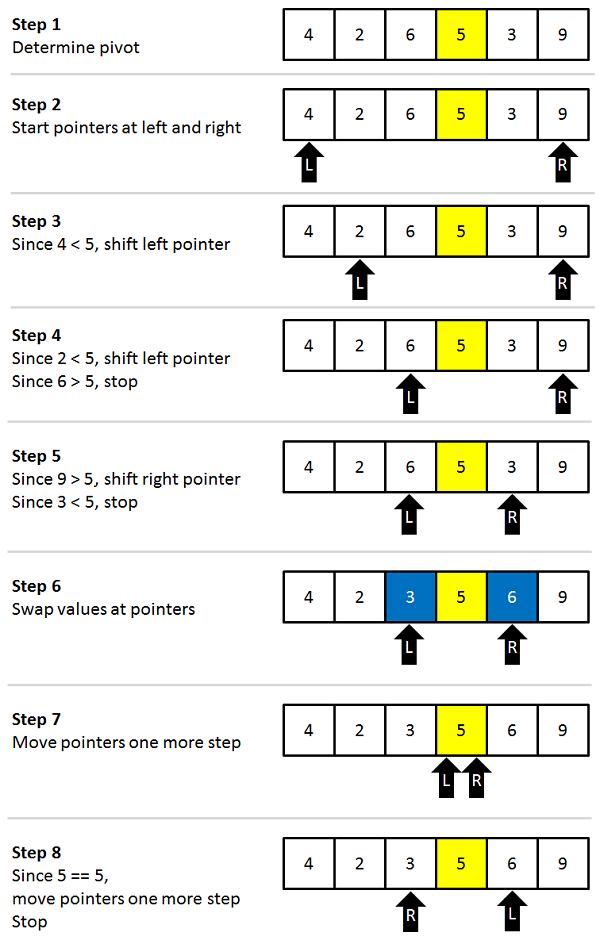
There are many approaches to calculating the pivot value. Some algorithms select the first item as a pivot. That’s not the best selection because it gives worst-case performance on already sorted arrays. It’s better to select a pivot in the middle of the array, so consider 5 to be the pivot value (length of array divided by 2). Next, start the left pointer at position 0 in the right pointer at position 5 (last item in the array). Since 4 is less than 5, move the left pointer to position 1. Since 2 is less than 5, move the left pointer to position 2. Now 6 is not less than 5, so the left pointer stops moving and the right pointer value is compared to the pivot. Since 9 is greater than 5, the right pointer is moved to position 4. The value 3 is not greater than 5, so the right pointer stops. Since the left pointer is at position 2 and the right pointer is at position 4, the two haven’t met and the values 6 and 3 should be swapped.

Next, the left pointer is increased by one in the right pointer is decreased by one. This results in both pointers at the pivot value (5). That signals that the operation is complete. Now all items in the array to the left of the pivot are less than the pivot and all items to the right of the pivot are greater than the pivot. Keep in mind that this doesn’t mean the array is sorted right now, only that there are two sections of the array: the section where all values are less than the pivot and the section were all values are greater than the pivot. See the figure below.

The implementation of a partition function relies on there being a swap() function, so here’s the code for that:

function swap(items, firstIndex, secondIndex){
    var temp = items[firstIndex];
    items[firstIndex] = items[secondIndex];
    items[secondIndex] = temp;
}

The partition function itself is pretty straightforward and follows the algorithm almost exactly:

function partition(items, left, right) {

    var pivot   = items[Math.floor((right + left) / 2)],
        i       = left,
        j       = right;


    while (i <= j) {

        while (items[i] < pivot) {
            i++;
        }

        while (items[j] > pivot) {
            j--;
        }

        if (i <= j) {
            swap(items, i, j);
            i++;
            j--;
        }
    }

    return i;
}

This function accepts three arguments: items, which is the array of values to sort, left, which is the index to start the left pointer at, and right, which is the index to start the right pointer at. The pivot value is determined by adding together the left and right values and then dividing by 2. Since this value could potentially be a floating-point number, it’s necessary to perform some rounding. In this case, I chose to use the floor function, but you could just as well use the ceiling function or round function with some slightly different logic. The i variable is the left pointer and the j variable is the right pointer.

The entire algorithm is just a loop of loops. The outer loop determines when all of the items in the array range have been processed. The two inner loops control movement of the left and right pointers. When both of the inner loops complete, then the pointers are compared to determine if the swap is necessary. After the swap, both pointers are shifted so that the outer loop continues in the right spot. The function returns the value of the left pointer because this is used to determine where to start partitioning the next time. Keep in mind that the partitioning is happening in place, without creating any additional arrays.

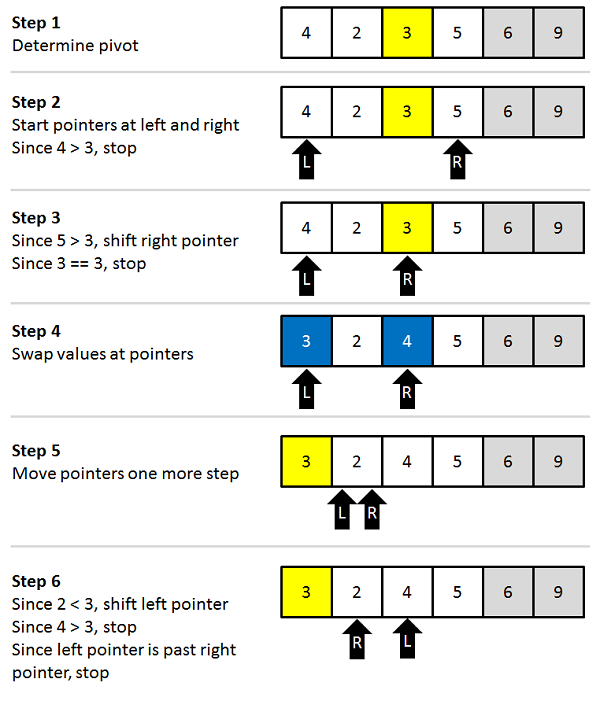
The quicksort algorithm basically works by partitioning the entire array, and then recursively partitioning the left and right parts of the array until the entire array is sorted. The left and right parts of the array are determined by the index returns after each partition operation. That index effectively becomes the boundary between the left and right parts of the array. In the previous example, the array becomes [4, 2, 3, 5, 6, 9] after one partition and the index returned is 4 (the last spot of the left pointer). After that, the left side of the overall array (items 0 through 3) is partitioned, as in the following figure.

After this pass, the array becomes [3, 2, 4, 5, 6, 9] and the index returned is 1. The heart rhythm continues like this until all of the left side of the array is sorted. Then the same processes followed on the right side of the array. The basic logarithm for quicksort then becomes very simple:

function quickSort(items, left, right) {

    var index;

    if (items.length > 1) {

        index = partition(items, left, right);

        if (left < index - 1) {
            quickSort(items, left, index - 1);
        }

        if (index < right) {
            quickSort(items, index, right);
        }

    }

    return items;
}


// first call
var result = quickSort(items, 0, items.length - 1);

The quicksort() function accepts three arguments, the array to sort, the index where the left pointer should start, and the index where the right pointer should start. To optimize for performance, the array isn’t sorted if it has zero or one items. If there are two or more items in the array then it is partitioned. If left is less than the returned index minus 1 then there are still items on the left to be sorted and quickSort() is called recursively on those items. Likewise, if index is less than the right pointer then there are still items on the right to sort. Once all this is done, the array is returned as the result.

To make this function a little bit more user-friendly, you can automatically fill in the default values for left and right if not supplied, such as:

function quickSort(items, left, right) {

    var index;

    if (items.length > 1) {

        left = typeof left != "number" ? 0 : left;
        right = typeof right != "number" ? items.length - 1 : right;

        index = partition(items, left, right);

        if (left < index - 1) {
            quickSort(items, left, index - 1);
        }

        if (index < right) {
            quickSort(items, index, right);
        }

    }

    return items;
}

// first call
var result = quickSort(items);

In this version of the function, there is no need to pass in initial values for left and right, as these are filled in automatically if not passed in. This makes the functional little more user-friendly than the pure implementation.

Quicksort is generally considered to be efficient and fast and so is used by V8 as the implementation for Array.prototype.sort() on arrays with more than 23 items. For less than 23 items, V8 uses insertion sort². Merge sort is a competitor of quicksort as it is also efficient and fast but has the added benefit of being stable. This is why Mozilla and Safari use it for their implementation of Array.prototype.sort().

Update (30-November-2012): Fixed recursion error in the code and added a bit more explanation about the algorithm.

References

1. Quicksort (Wikipedia)
2. V8 Arrays Source Code (Google Code)

Disclaimer: Any viewpoints and opinions expressed in this article are those of Nicholas C. Zakas and do not, in any way, reflect those of my employer, my colleagues, Wrox Publishing, O'Reilly Publishing, or anyone else. I speak only for myself, not for them.